ARIMA-1 Stationarity and Difference
Contents
ARIMA模型为时间序列预测提供了另外一种方法。在时间序列预测中exponential smoothing和ARIMA是两种最常用的模型,它们对于同一个问题具有互补的优势。Exponential smoothing模型可以描述数据中存在的trend和seasonality,而ARIMA模型可以描述数据中存在的autocorrelations。
1. Stationarity
一个stationary时间序列的性质和观察它的时间点无关,也就是它没有trends或者sensonality,因为trend和seasonality会在不同的时间点影响这时间序列的取值。比如white noise就是一个stationary序列,它的性质和你什么时候观察他没有关系。其实一个有这cyclic behaviour(but with no trend or seasonality)的时间序列也是一个stationary序列,这是因为cycles没有固定的长度,我们无法判断一个cycle的峰和谷。这里stationary序列指的是稳定序列,稳定序列的特性就是不受时间维度上各种特征的影响,之和自己之前的取值有关,这其实也是ARIMA算法的基础。比如股票数据一般来说其实就是不稳定数据,因为它常常受到政策,新闻或者整个经济大环境的影响。
一般来说,stationary序列就是那些在long-term中没有predictable patterns的序列。下图是一些时间序列,请分析以下它们所属的类型,是不是stationary序列。
- (a) 连续200天的谷歌股票价格
- (b) 连续200天的谷歌股票价格的变化
- (c) 美国每年恶性袭击的案件数
- (d) 美国独栋别墅的月销量
- (e) 美国一打鸡蛋的年平均价格
- (f) 澳大利亚每个月杀猪量的总和
- (g) 澳大利亚每年捕获猞猁的总量
- (h) 澳大利亚每个月的啤酒产量
- (i) 澳大利亚每个月的供电量
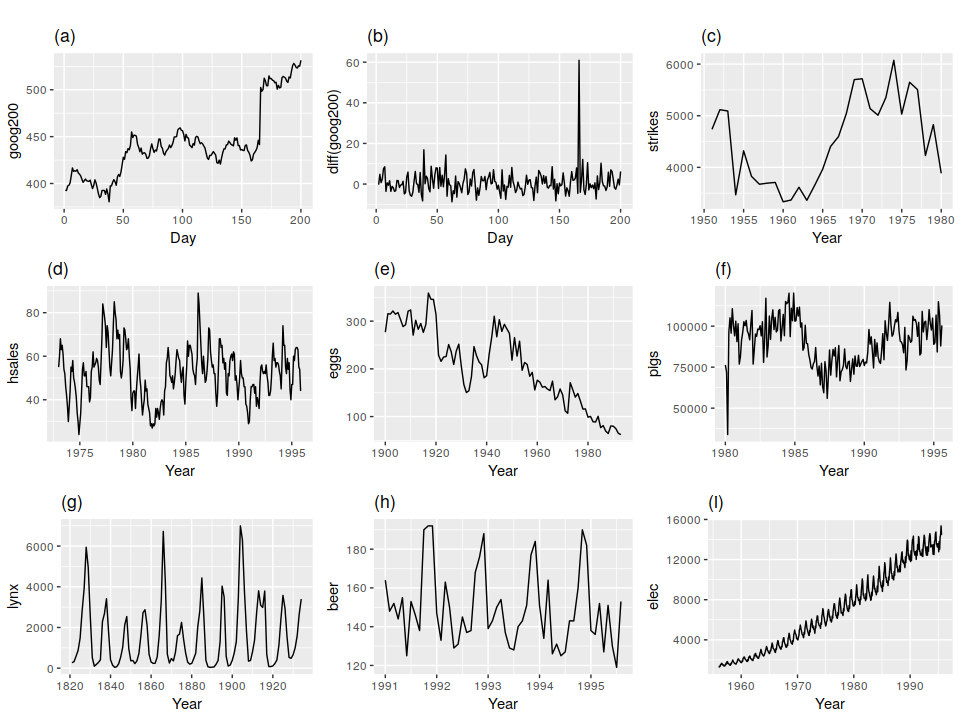
分析上图中的9个时间序列,很明显图(d),(h),(i)具有很强的季节性seasonality;图(a),(c),(e),(f),(i)具有很明显的趋势trends;图(i)的表现是方差越来越大;所以只剩下(b)和(g)是stationary series。乍一看好像图(g)表现出的cycles会使得它成为non-stationary序列,但是仔细观察发现这种cycles是aperiodic,所以在long-term内,这些cycles是无法预测的。
2. Differencing
在上图中,(a)图是non-stationary,但是(b)图是stationary,这就提供了一种把序列从non-stationary转化到stationary的方式,就是计算连续观测值之间的差异,叫做differencing。Differencing can help stabilise the mean of a time series by removing changes in the level of a time series, and therefore eliminating(or reducing) trend and seasonality.
使用ACF plot的方式可以有效地判断non-stationary时间序列。对于一个stationary时间序列,ACF will drop to zero relatively quickly while ACF of non-stationary data decreses slowly. 下图是谷歌股票价格和股票价格变化的ACF图。
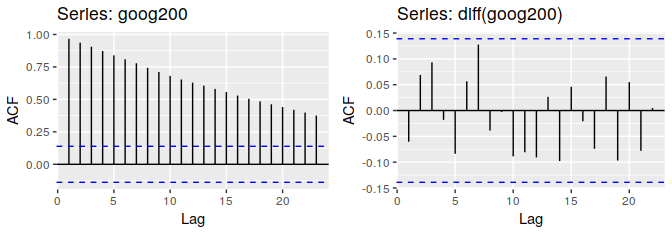
则由上述讨论可知每天股票价格的变化是一个随机变量,并前几天没有什么相关性。
3. Random walk model
上面提到的差异序列(differenced series)其实是原始序列的连续观测值之间的差值构成的,所以可以表达成如下形式。
$$
y_t^{‘}=y_t-y_{t-1}
$$
所以对一段长为$T$的序列来讲,它的差异序列的长度只有$T-1$个值。当差异序列是白噪声的时候,原始序列的模型可以用如下方式表达。
$$
y_t-y_{t-1}=\epsilon _t
$$
这里$\epsilon_t$表示白噪声,重新整理上式就得出了random walk随即游走模型。
$$
y_t=y_{t-1}+\epsilon_t
$$
随机游走模型在non-stationary序列数据中有着广泛的应用。一般随机游走具有以下特点:
- long periods of apparent trends up or down
- sudden and unpredicted changes in direction
使用随机游走模型的预测值等于时间序列的最后一个观测值,因为继续随机游走的时候是unpredictable的,equally to be up or down。所以,随机游走模型underpins naive forecast method。一个类似的使得differences有非0均值的模型如下。
$$
y_t-t_{t-1}=c+\epsilon_t \quad \text{or} \quad y_t=c+y_{t-1}+\epsilon_t
$$
这里的$c$是连续观测值之间变化的均值。如果$c$为正数,则平均变化值相对于$y_t$上升了,即$y_t$ will tend to drift upward,否则,$y_t$ will tend to drift downwards。则这时模型类似于drift method。
4. Second-order differencing
有时differenced series还是没有表现出stationary的性质,这时候就很有必要再做一次difference以期待得到stationary序列。则有如下二阶差异:
$$
\begin{aligned}
y_t^{‘’} & =y_t^{‘}-y_{t-1}^{‘} \
& = (y_t-y_{t-1})-(y_{t-1}-y_{t-2})\
& = y_t-2y_{t-1}+y_{t-2}
\end{aligned}
$$
这种情况下,$y_t^{‘’}$有$T-2$个值,在实际应用中,我们几乎不会使用大于second-order的differences。
5. Seasonal differencing
周期性差异指的是当前观测和同周期的前一个观测之间的差异,可以如下表示。
$$
y_t^{‘}=y_t-y_{t-m}
$$
这里$m$表示周期的个数,上式也叫做lag-m differences。如果周期性差异数据是白噪声的化则有如下模型。
$$
y_t = y_{t-m}+\epsilon_t
$$
则这个模型和naive forecast method是一样的。同第4小节中的二阶差异一样,周期性数据也存在二阶差异使其变成stationary数据。
6. Unit root test
决定一个序列是否需要differencing的一种方式是unit root test单位根检验,这是一种决定是否应该使用differencing的假设检验方法。已有很多单位根检验方法,在这种假设检验中,空假设是数据是stationary的,如果假设被拒绝,则需要使用differencing方法,如果假设被接受则不需要。